[ PDF version ]

[ PDF version ]

[ PDF version ]

[ PDF version ]

Download my 167-page
report: Special Operations
in Medical Research
[pdf – 1.88MB]:

Download my Open Letter to the British Prime Minister & Health Secretary
[pdf – 363KB]:

The Limits of Rationality
(An important mathematical oversight)
[863KB]:

Radical Affinity and
Variant Proportion in
Natural Numbers
[2.53MB]:

Mind: Before & Beyond Computation
[643KB]:

Dawkins' Theory of Memetics – A Biological Assault on the Cultural
[508KB]:

Randomness, Non-
Randomness, & Structural Selectivity
[616KB]:

Randomness, Non-Randomness, & Structural Selectivity

In my critique of Dawkins' theory of memetics I had concentrated on what I saw as the rather problematic decoupling of evolutionary theory from biology and its grafting onto cultural practices – the exchange of ideas – by force of analogy. I did not attempt a substantial critique of the theory of evolution on biological terms as I do not feel qualified to do so. Nevertheless, that essay had taken one of its cues from a quote by William James (1880)¹, expressing his distrust for the quasi-scientific “metaphysical creed” which he understood as the impetus behind late nineteenth century trends in evolutionary ‘philosophising’, and which he saw as being sustained independently of the empirical study of particular examples of species change. Today, evolutionary theory is adopted by many non-scientists and scientists alike as the standard narrative explaining man’s (even woman’s too) relationship to his distant prehistorical past. It remains however a substantive critique that much of the energy and impetus behind evolutionary models of thinking derives not directly from the evidence of empirical observation, but from an abiding attachment to a powerful explanatory model; one which manifests itself with all the compulsion of a fully-fledged belief system. In the prevailing orthodoxy of combined expert and inexpert opinion, it seems that some of the central tenets of evolutionary theory have survived, since Darwin’s publication of On the Origin of Species by Means of Natural Selection (1859), with inadequate criticism or refinement. In consideration of the fact that Darwin’s publication occurred a century prior to the discovery of DNA, the genetic code-substrate, it seems reasonable that the theory of evolution by natural selection should be subject to some reflective revision in the light of that discovery.

In spite of prodigious attempts to document the contents of the human genome, the mechanisms of gene expression within DNA remain largely a mystery to biologists. At the same time, textbook evolutionary theory, particularly that of the latter 20th Century, has assumed orthodoxy based exclusively upon the principle of natural selection as the sole determining factor in species change. This is in spite of the fact that Darwin himself made no such ambitious claims for his theory. If one reads the final chapter (14) of the On the Origin..., one has the impression of something left incomplete – in anticipation of future refinement or revision. Darwin’s observations and speculations on the phenomenon of species change were indeed challenging enough at the time, because they showed strong evidence that species were not fixed designs – they were mutable, and therefore clearly not the result of spontaneous creation. The ensuing struggle with Creationism has completely polarised the debate, and has meant that Darwinism has tended to resort to a defensive retrenchment around a set of rather nebulous, in fact prematurely retarded, inductive-deductive principles. The debates with creationists still continue to this day, with the result that Neo-Darwinism maintains this combative attachment to the logical simplicity and explanatory power of Darwin’s nascent principles.

The theory of natural selection specifies that all molecular genetic change occurs isomorphically, that is, in all directions equally, without determination towards specialisation of form, and without by itself selecting in favour of any consequential benefit to the host organism. All selection, that is, takes place at the environmental level, through the tempering of putatively ‘random’ genetic mutations according to the advantages (or disadvantages) they confer upon organisms in terms of their competitive survival. Natural selection is a theory derived on the basis of the available visible evidence, which for Darwin consisted in an inexhaustible catalogue of taxonomic observations, together with a rather impoverished, or incomplete, palaeographic (fossil) record. That is to say that the theory developed in ignorance of the existence of a substantive mechanism or structure (that of DNA) underlying genetic change, and so naturally pursued its causal explanations at the level of the visible – those of the observed (or inferred) interactions of phenotypes with their environments – whence it at least had the capacity to make substantive observations.

One of the most pervasive critiques of Neo-Darwinism has been that of Stephen Gould’s seminal work, The Structure of Evolutionary Theory². Gould’s mammoth project, impressive in its scope and erudition, is to preserve a differential theoretical understanding for a range of processes affecting evolutionary change; to undo some of the reductionism of the 20th Century synthesis of evolutionary theory to the ‘one level’ algorithm of natural selection. The motivation for this is partly a respect for Darwin’s early efforts, and partly also a sensitivity that Darwin’s theories have been co-opted by reactionary social agendas, notably those which have sought scientific support in favour of racist, evolutionary-supremacist, and eugenicist ideologies and programs. Gould claims that there are important aspects of large-scale evolutionary phenomena, such as macroevolution, extinction, and species-drift, which are inadequately explained in terms of natural selection alone. He does not challenge the theory of natural selection on principle, but rather its overemphasis in orthodox Neo-Darwinist accounts. One of the problems resulting from this overemphasis is that insufficient attention is paid to the importance of structural constraints upon the form and direction of an organism’s evolutionary development. Gould generally ascribes to a theory of molecular genetic change as essentially a random process; although he makes a valuable distinction between ‘technical’ and ‘vernacular’ uses of ‘randomness’. For instance, technically speaking, if a process occurs randomly the implications are not (as in the vernacular sense) that it tends towards disorder and chaos, but rather that prevailing conditions are essentially even, or uniform, and do not influence the process with any especial inclination to go one way or another:

“In ordinary English, a random event is one without order, predictability, or pattern. The word connotes disaggregation, falling apart, formless anarchy, and fear. Yet, ironically, the scientific sense of random conveys a precisely opposite set of associations. A phenomenon governed by chance yields maximal simplicity, order, and predictability – at least in the long run. Suppose that we are interested in resolving the forces behind a large-scale pattern of historical change. Randomness becomes our best hope for a maximally simple and tractable model.”³ (his emphasis)

Gould is a palaeontologist, rather than a geneticist, and so his critique of orthodoxy is concentrated on stochastic analyses of evidence available from the palaeographic record, which might furnish only indirect clues regarding molecular processes. However, the suggestion that randomness is the principle that offers the “best hope” for a managed understanding of natural processes, says more perhaps about the nature and limitations of scientific methodology, than anything definitive about natural processes themselves. Seemingly, ‘randomness’ is taken as a baseline inference upon which to construct a coherent theory, and one upon which data may be more readily subjected to quantitative analysis; that is, by presupposing that basic conditions are even and consistent, and do not influence natural processes with any particular inclination or tendency. It is on this point that I think evolutionary theory most consistently fails to subject its own terms of analysis to reflective self-criticism.

Induction and Reduction

Rational scientific thinking interprets the biological features of Nature as organic responses to changes in physical and chemical conditions which themselves behave according to a set of fixed and determinable laws, and which are uniform, or universal. If the laws of Nature operate universally, then unconventional changes in natural forms must have their origin in some form of accidental irruption of those laws. The development of evolutionary theory in the 19th Century was hampered by the fact that genetic processes were in themselves largely unfathomable, except insofar as they resulted in macroscopic changes in phenotypes. This naturally led to an emphasis upon evidence of observable changes in biological organisms, principally by reference to fossils in the palaeographic record. The interpretation of these changes hence became divided between: a) a theory of change as an elective internal response to external environmental conditions (i.e., as predictable, and with a constructive influence in terms of an organism’s will to survive, and which might result as a consequence of the pressure of habitual patterns of behaviour); and: b) change as an environmentally tempered response to an unpredictable and isomorphic internal process that, given the limitations of empirical observation, remained largely a mystery, but which tended to satisfy the preference for an explanation involving chance or accident as the originating cause. These twin theoretical priorities were characteristic of the debate between Lamarckian adaptive principles on the one hand, and the principles of Darwinian natural selection on the other.

The Darwinian preference for an explanation of biological changes in terms of an internal process which in itself is fairly indeterminate grew in response to the requirement for an explanation for why, on the one hand, there is clear evidence of progressive refinement in the adaptability of species to their environments, yet, on the other hand, certain genetic changes result in mutations and deformities which offer nothing of benefit to the organism. Although the systems of genetic inheritance are complex and structured, as Mendel showed, the generative basis of genetic change (and ultimately of evolution) is accidental variation at the molecular level. These variations are then tempered, or selected, at the environmental level, according to their relative fitness for survival; mutations which do not facilitate enhanced survival chances are de-selected, or ‘weeded-out’, for the reason that those organisms will have a relatively reduced opportunity to reproduce and pass on their variations.

This presumption of an essentially random process lying at the roots of genetic change is really an aspect of science trying to conceptualise what lies beyond the limits of its observation. If we cannot observe what happens at the genetic level, we cannot derive laws to explain that behaviour, and so these phenomena must be consigned to a place beyond the law, as accidents or anomalies – a tendency encouraged by the awareness that a significant portion of (especially the visible) genetic mutations are disadvantageous, or indeed monstrous. This is where rationality imposes its distinction – as disadvantageous mutations occur with frequency, then genetic change appears de facto to be a generally non-selective process. As we can readily observe the effects of non-fortuitous mutations from repeated and successive examples before us, we reason by induction that all such change occurs on the same indeterminate principle.⁴ Henceforth we have inductively eliminated any other possibility from the equation (arguments in favour of Lamarckian principles notwithstanding). Such elimination is necessary as the general status of scientific knowledge (for example the non-discovery of DNA during the 19th Century) permits of no further complexity in the argument.

Randomness, therefore, is an approximation (by reduction) to an analysis of what is going on at the molecular level; that is, it was the closest that rationality could get to an understanding of the process, given the limited state of empirical knowledge at the time; and given the paucity of the geological record from which much of Darwin’s evidence was taken. The implication, which ought not to survive an attempt at explicit theorisation, but which nevertheless has tended to become adopted as baseline evolutionary commonsense, is that genes exist in a sort of ‘soup’, and that their combinations and re-combinations occur essentially chaotically – by accident. If it were to happen any other way, by some principle of ‘guided design’, or by an ordered or non-random process, then how do we explain the propensity towards ‘freakish’ mutations?

There are reasons why the discovery of DNA might have undermined this assumption of randomness, which I will attempt to explain. But the fact that it hasn’t (at least for a large proportion of evolutionary biologists) points to a failure of reflective criticism in the debate, and an over-tenacity for inherited scientific orthodoxy, the motives for which are anything but scientific. There were, undoubtedly, influences upon the development of Darwin’s theory, and upon the orthodoxy that succeeded it, which were epistemic and moral rather than empirical – on the one hand a preference for forms of mechanical explanation based upon the uniformity of physical and chemical laws interrupted by moments of chaos; and on the other hand, a desire for natural laws which could be re-interpreted and translated into social and moral prescriptions, for the perceived betterment of society, and as a solution to impending social ills.

In addition to this influence of epistemic and moral factors, Rebecca Stott’s fascinating history of Darwin’s engagement with the barnacle species, Darwin and the Barnacle⁵, presents a rare insight into Darwin’s methodology, as a struggle between the compulsive pursuit of an hypothesis about the development of species through environmental adaptation on the one hand; and, on the other, a series of interminable frustrations to the finalisation of this ‘big idea’, in part circumstantial, but largely due to the difficulty in isolating consistent empirical data regarding the barnacle species which might ensure an unequivocal confirmation of Darwin’s central hypothesis. Stott presents a vast amount of biographical detail which brings into relief the analogy between the characteristic urgency and compulsion of Darwin’s scientific speculations – his need to cash-out the theory of natural selection in a way robust enough to make a meaningful impression upon the scientific community – and his considerable financial investments in the railways, so that his theoretical speculation takes on the character of an ‘investment’, which entails its own momentum and commitment, to be pursued, if necessary, ‘against the odds’:

“The same [financial-speculative] instinct for risk would be needed for the publication of his species theory, of course: knowing when enough facts constituted a general law, and then knowing precisely when to try out that general law on the readers who would be its judge and jury. Once that move had been made, there would be no way back.”⁶

Importantly, at the time of Darwin’s publication there was little available evidence that might support a theory that embraced the possibility of determinacy in internal processes, due to the fact that DNA was unknown; and, due to the political imperative of cashing-out evolutionary theory as a logically consistent hypothesis, the whole issue of randomness/non-randomness was overlooked. And this situation has continued, because science habitually looks for the most reductive form of explanation. It supposes that there must be a neutral or value-free level of description. But supposing that there are complexities in the functional mechanisms of DNA molecules that we are still unaware of, why should evidence of non-randomness in DNA be self-evident? After all, the evidence which Darwin used was not self-evident – it required interpretation; and the theory which resulted was a highly selective interpretation. Darwin’s theory was informed first of all by reflections on economic and social policy in the context of population dynamics, in the wake of Thomas Malthus’ An Essay on the Principal of Population (1803)⁷; and as a conscious analogue to the economic theories of Adam Smith⁸; that is, it began from a concern which was value-laden. In other words, Darwin’s theory gained impetus from the pressing concerns of his social milieux. After all, science does not develop in a vacuum, and the persuasive import of the theory was perhaps more a factor of its application by analogy towards a renewed perspective on pressing social concerns, than that of its nominal application to an understanding of strictly biological processes.

There are, in particular, two serious consequences that follow from the assimilation of the biological mechanism of natural selection into social and moral prescriptions. Firstly, where selection occurs solely on the basis of relative fitness for survival, the modality for progression of the species comes down to an aggressive contest between individuals, the benefits of which when applied to the social sphere are ultimately ambiguous, or regressive. If the metaphor of natural selection is applied as a means of underwriting patterns of social or commercial interaction, what is sanctioned is the most extreme form of aggressive individualism, where individual goals (or perhaps kinship goals) are pitted against the goals of broader social groups. Secondly, differential survival chances result from the inheritance of previously tested genetic mutations, which places special emphasis on the mechanisms of inheritance. But in a civilised society in which the factor of naked survival through biotic competition is largely removed, natural selection no longer ‘weeds-out’ bad genes. Consequently, the inheritance of deleterious genetic traits gains priority as the scientific explanation for a panoply of human social, and especially behavioural, problems. Theories of genetically inherited personality, intelligence, criminality, or ‘imbecility’, for instance those initiated by Francis Galton (Darwin’s cousin), and which were the progenitors of eugenics. Generally speaking, 20th Century sociology and psychology academicians were to have enormous difficulty extricating those discourses from the biological determinism which sought causal explanations for an entire spectrum of human behavioural and character traits in mechanisms of genetic inheritance. Bearing in mind the inadequacy, from our own historical perspective, of the 19th Century taxonomical distinction between the categories species and races, the sociological import of Darwin’s new theory is expressed in the subtitle of his major work: On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. As a successor to On the Origin..., Darwin also attempted a comparative taxonomy of human and animal emotions, as exhibited through facial expressions; as if the intricacies of human personal interactions might conceivably be better understood through a series of face-behavioural stereotypes.⁹

The Structure of DNA

The discovery of DNA in the 1950s was an opportunity for a significant revision of the central tenet of molecular randomness as the generative basis of genetic change. The DNA molecule clearly exhibits a three-dimensional structure (the double-helix), as well as identifiable code elements (in the distribution of AGCT nucleotide groups). From the perspective of a genetic understanding of biological development, it is the arrangement and combinations, the presences and absences, of identifiable groupings of these elements that determine the structure and characteristic features of phenotypes (physical organisms). If the presupposition of randomness in genetic mutation is to be maintained, and if it is also maintained (as the theory of evolution by natural selection requires) that all determining factors in species change arise externally, from the interaction of phenotypes with their environments, then we must exclude from the equation any positively developmental contribution arising as a factor of the biochemical activity of DNA within the nuclei of cells. We must exclude, that is, the possibility of cumulative change over time where the succession of changes occurs purely as an effect of structurally imposed constraints upon the pathways of development for the various novel generations of muscular, skeletal, and nervous tissue that organisms may acquire. In addition to that, we must also exclude the possibility that modifications to DNA arise in response to changes in patterns of behaviour during the lifetime of the organism, perhaps reflecting enhancements in its physical or intellectual capacity, and which are subsequently assimilated dynamically into its genetic code, and passed on to its offspring. As we do not yet possess any complete or definitive understanding of the mechanisms of DNA and RNA in the synthesis of proteins, nor of the respective roles of either in instantiating the genetic code, such exclusions seem unjustified, or at least unwise.

It would be equally unwise to exclude the principle of natural selection itself as a contributing factor amongst a series of other differential factors in any comprehensive understanding of the processes affecting the descent of organisms with modification. However, within mainstream biology such non-reductive approaches to the subject are treated as ‘heretical’, and subjected to academic ridicule, because they undermine the coherence and rectitude of the established scientific paradigm. To return to Gould’s critique, it is the overemphasis on natural selection in orthodox Neo-Darwinist accounts, to the exclusion of all other factors, which presents the greatest obstacle to a deeper understanding of the subject. To add to Gould’s critique, the failure to reflect upon the question of how the structural properties of DNA might constitute a positive developmental effect upon changes within the genetic code is a symptom of the general unwillingness to revise commonly held principles that serve to entrench established orthodoxies. In this context, the most prevalent of these is the intractable principle of molecular randomness as the indeterminate condition underlying changes in the genetic code.

There are various ways in which DNA could be analysed. The three-dimensional structure of the molecule and the spatial positioning of elements within this structure I understand to be of crucial importance. However, most DNA analysis, including the representation of the elements in charts, is conducted linearly. This is again a form of reduction, which to an extent precludes an understanding of the relevance of the spatial positioning of elements within the structure. Viewed reductively as a linear-sequential series of coded elements, DNA may be considered as a ‘symbolic system’; by which is implied that individual elements, or groups of elements, possess a combination of ‘semantic’ properties (i.e., the ‘meaning’ that the presence of individual code elements signifies in terms of corresponding physiological properties observable at the level of the phenotype); as well as ‘syntactic’ properties (in that individual elements exist according to a set of biochemical dependencies, and are internally recognisable as biochemical indicators). Although the number of active elements is limited to the four nucleotide groupings: Adenine, Guanine, Cytosine, and Thymine; their combinatory potential is significantly more numerous. It is likely that, even in this reductive (linear) representation of DNA structure, it already exhibits properties and behaviours that are comparable in principle to those of any symbolic language (bearing in mind that we use this word to describe not only human discourse, but also the codebases in which computer programs are written). We have no reason not to expect that DNA is a functional medium with both semantic and syntactic properties, such that it may be analysed according to principles comparable to those applied to a variety of linguistic code structures. This is before we even consider the three-dimensional spatial structure of the DNA molecule.

Let’s try to define exactly what is implied by the inference of ‘randomness’, and whether the concept of indeterminate variation is at all applicable within a medium as evidently structured as a DNA molecule. If we take the classic example of the throwing of a die, there are six evenly balanced options (assuming the die is ‘true’), and if one throws the die a sufficiently large number of times, each of the six options will approximate to an equal numbers of outcomes – for 600 throws we should expect to get something like 100 ‘1’s, 100 ‘2’s, 100 ‘3’s, and so on. In any practical demonstration however it is extremely unlikely that they will fall exactly equally. Presumably, the greater the number of throws, the more even the distribution will be. So, randomness may apply as the ideal limit of systems entailing freely selective options under truly neutral conditions. Are DNA molecules examples of this kind of system? And do they operate within truly neutral conditions (internally or externally)?

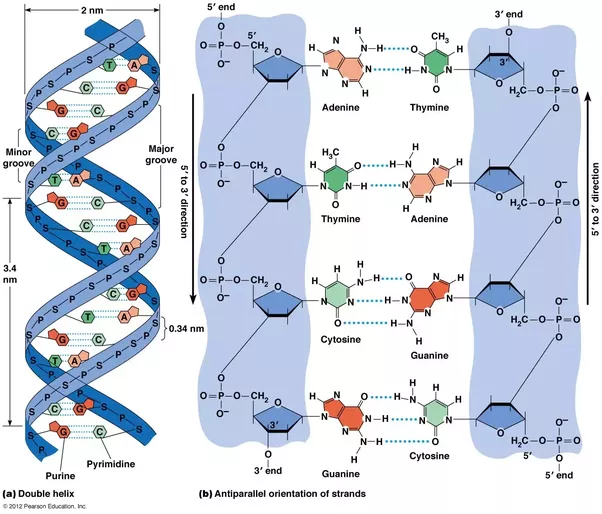
Composition of the rungs of a DNA helix
(click to expand – source: Quora.com)

In response to the first question, as a three-dimensional structured matrix DNA does not exhibit the ideal form of a neutral pool (as in the ‘soup’ analogy) of freely optional elements – the elements cannot be conceived as having equal status, in terms of the probability of one element being replaced by any other; that is, they are not freely selectable according to a system of rational equivalence, as in the case of the throwing of a die. The elements of a DNA matrix are not free-floating, or freely interchangeable, and are determined by fairly strict biochemical dependencies (there are required pairings between Guanine and Cytosine groups, and between Adenine and Thymine groups, and these pairs are systematically alternated, for instance). That is to say that the inference of randomness in genetic mutation ignores those structural determinations which will inevitably apply to any given position within the given three-dimensional syntax of the DNA molecule.

In response to the second question, the external environment of a DNA molecule is the cell, beyond that, the specific organ, then the body of the organism, then its external environment. Functional changes within DNA molecules are influenced by the chemical balance of cells, which in turn is affected by nutritional components, the constitution of free radicals, by the balance of homeostasis, and by the relative efficiency of apoptosis (programmed cell death), etc. These are all in turn affected by the external environment of the organism, its diet, the proximity of infection, by prevailing electromagnetic radiation, and not least by the organism’s emotional disposition. At the point of conception of an embryo, none of these conditions could be described as operating neutrally, as in the case of clinically- or experimentally-controlled conditions.

With regard to the internal conditions of DNA molecules, as a structured three-dimensional matrix of elements exhibiting syntactical dependencies, we cannot describe the internal conditions of the molecule as in any way uniform. The molecules have directional polarity – they are not equilateral, and there is a predetermined order and sequence to their physiochemical behaviour. They cannot be conceived in any way as possessing the characteristics of material homogeneity or evenness of the kind that enables us to evaluate the internal structure of the die, for instance, as disinclined (or ‘true’). If a DNA molecule exhibits a capacity towards internal change, then it is likely that these changes occur according to a process that has the characteristics of selectivity – that is, for configurations that are possible and against those that are impossible – criteria that will vary according to existing configurations, and which implies that mutations will progress cumulatively. If mutations progress cumulatively according to existing configurations, then such changes are being determined internally according to a non-random process, presumably with the capacity to exploit or to promote patterns of physiochemical affinity between individual code elements. This is tantamount to saying that DNA molecules exert an internal ‘design’ function, and which may contribute to the establishment of developmental pathways, which in turn will determine macroscopic features of phenotypes (by saltation that is, rather than isomorphically according to the principle of natural selection).

The point is that it really makes little sense to talk of ‘random’ or ‘accidental’ variation applied to a system where there are significant structural and biochemical determinations at play, and where changes occur cumulatively. We are dealing with a system which, to all intents and purposes, is so thoroughly determined, even in its variations, that to define those changes as in any way ‘random’ amounts at best to an oxymoron, at worst to pure mystification.

In view of what was said above in relation to the influence of external factors, it is important to recognise that there may be contributions from extra-cellular factors which influence genetic change disproportionately, and which may propitiate certain kinds of non-fortuitous mutations. This suggests the need for some kind of qualitative distinction between cumulative or saltational genetic changes generated internally, and those that appear as aberrations due to external pressures. The premises which inform the principle of exclusive natural selection however cannot but remain insensitive to this distinction.

Non-Randomness

It seems to me therefore that most of the structural properties of DNA molecules are overlooked when it comes to the assertion that genetic variation occurs on a random basis. A probable reason for this oversight is that of the lack, within conventional biological discourse, of a suitable conceptual model for analysing the distinction, suggested in the previous section, between the semantic and the syntactic properties of DNA molecules. Hence the need for an interdisciplinary approach, which borrows from linguistics certain analytical categories, based upon a putative but not unreasonable analogy between the structure of DNA and linguistic code structures. In referring to ‘syntactic properties’, I am identifying a distinction between the sequential dependencies of elements according to their position within the three-dimensional structured matrix on the one hand, and, on the other hand, the functional properties of isolable elements, or groups of elements, in terms of what they signify for the macroscopic structure of the phenotype (the latter which linguistics would identify as ‘semantic’ properties). Syntactic properties imply that one cannot reasonably understand the role of elements or groups in terms of their absolute presence or absence within the molecule (i.e., with the potential of occurring or not occurring randomly), abstracted as it were from their relative positions and biochemical dependencies within the matrix. These positions indicate a series of syntactic relationships, locally and globally, and which determine a range of possibilities, as well as impossibilities, in terms of the occurrence or substitution of elements for any particular position in the molecule. If certain configurations are excluded a priori on the basis of the existing internal configuration, then the options for change by substitution are limited and determinate, rather than limited and random.

In referring to the DNA matrix as a ‘symbolic system’, it is implied only that individual elements – AGCT nucleotide groups – have meaning or significance in terms of the functional role they play in the molecule as a whole, and that they are internally recognisable as biochemical signals. At its simplest a symbolic system may comprise a simple distinction, as in binary notation, between positive and negative, or the logical distinction ‘true’ and ‘false’. DNA is considerably more complex symbolically than this; but it is helpful to take the example of a binary system of notation as a baseline category for an analysis of symbolic systems in general in terms of their capacity for randomness.

In what follows I am indebted to Bruce Fink for his representation of the findings of Jacques Lacan¹⁰, following Lacan’s description of a rudimentary artificial language of syntactic codes based upon an elementary sequence of coin tosses. Following Lacan’s system of notation, Fink represented the results of a sequence of nine coin tosses, assigning a ‘+’ for ‘heads’, and a ‘–’ for ‘tails’. He then grouped sequential pairs of coin tosses according to three types:

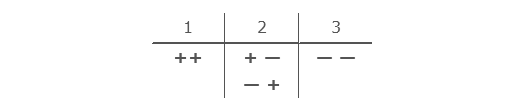
So that a typical sequence of coin tosses might look like this:

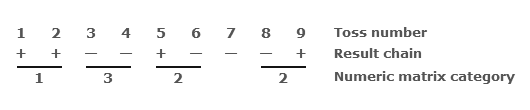
The ‘numeric matrix category’ describes the characteristics of pairs of sequential tosses by encoding an additional symbolic layer, which categorises them according to types 1, 2, & 3 as defined in the first table, but which can be understood in terms of a level of functional description.

Fink then applied the same categories to overlapping pairs:

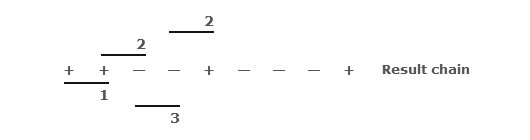
Compressing these results into a single display gives:

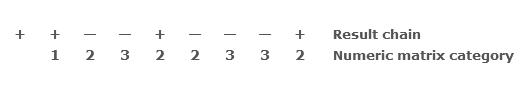
Each number in the numeric matrix category signifies the type of sequential pair composed of the result immediately above it and the preceding result. What this minimal symbolic encoding establishes is that following a ‘1’ in the matrix chain, one cannot have a ‘3’ without an intervening ‘2’; and similarly, following a ‘3’ one must have a ‘2’ before a further ‘1’ may appear. So, by abstracting by one level of functional description from the baseline random series, we have already introduced a factor of restrictive determination into the series which renders certain configurations possible and others impossible (for example, 1,2,1 is possible, but 1,3,1 is not; 3,2,1 is possible, but 3,1,2 is not).

Lacan was principally concerned with an examination of how language develops signifying chains where the possibilities of use are dictated by rules which emanate purely from within the code itself, as it were unconsciously; to counteract the assumption that the rules are formed overtly, on the basis of a direct reciprocal correspondence between language and the objects it represents. For instance, in the above example, the fact that certain combinations appear impossible dictates nothing about what we should expect from the sequence of coin tosses itself. The restrictions manifested by this expression of elements of the symbolic code do not arise as a reflection of behaviour in objects at the empirical level. The implication being that any language, as exemplified in this minimal abstraction from the sequence of real events (coin tosses) to the most basic level of symbolic description, will determine conditions for its use that seem to emanate ex nihilo¹¹. A further observation from the above example is that, where a ‘2’ (or a ‘3’) follows upon a ‘1’ in the numeric matrix, a subsequent ‘1’ cannot arise until an even number of ‘2’s has occurred. In view of this behaviour Fink states:

“[...] that the numeric chains “keep track of” numbers, that in a certain sense they count them, not allowing one to appear before enough of the others, or certain combinations of the others, have joined the chain. This keeping track of or counting constitutes a type of memory: the past is recorded in the chain itself, determining what is yet to come.”¹² (his emphasis)

Lacan’s experiment helps to illustrate that, even for a set of outcomes as ostensibly random as the results of a series of coin tosses, the analysis of the series in terms of a rudimentary level of functional description (at one level of symbolic abstraction) introduces relations of syntactical dependency that determine outcomes among isolable functional groupings in terms of the possibility or impossibility of those outcomes with respect to what has previously occurred. However, there is a degree of independence between the raw series of coin tosses and its functional description, such that the laws of possibility arise discretely from within the code itself, rather than being directly determined on the basis of actual events.

In suggesting that DNA might be better understood through the application of linguistic methods of analysis, we are suggesting that the functional properties of DNA elements (what those elements might determine with respect to the observable characteristics of phenotypes) correspond to the meaning-bearing, or semantic, properties of language as a system of codes. The double helical structure of the DNA molecule, as a physical structure, and existing physiochemical dependencies between isolable code elements, correspond to the syntactic properties of DNA. In linguistic analysis, semantic and syntactic rules are understood to operate quasi-independently. There is a degree of opacity between the two sets of rules, so that one cannot understand syntactic determinants purely within the terms of semantic ones, and vice versa. The general inference from this position is that there is no 1:1 relationship of transparency between any system of codes and the objective reality those codes purport to represent; and this applies whether we are considering either natural or artificial languages, or indeed the interpretation of DNA functional elements in terms of how they determine the macroscopic structure of phenotypes. So, while the observable evidence of non-fortuitous mutations in living organisms might encourage the impression that genetic change appears to manifest itself randomly and unpredictably, on the analysis of the syntactic behaviour of code structures, it is misguided to interpret the appearance of randomness at the macroscopic level as a ‘reflection’ of corresponding random manipulations of the genetic code.

I have used Fink’s representation of Lacan’s experiment only to illustrate a very basic point about code structures. The observable characteristics of living organisms do not permit a direct comparison with an unstructured sequence of coin tosses. In addition, AGCT groupings within DNA are not purely symbolic items – there are chemical dependencies in the sequence of nucleotides that might exclude certain categories of pairs per se. The fact that AGCT groups are already functionally significant means that we do not need to make an initial abstraction into the symbolic, such as in Fink’s ‘numeric matrix category’. However, the three-dimensional structured matrix of a DNA molecule prescribes a set of syntactical dependencies for isolable functional groupings situated within it, and the model described above does have general applicability in showing that functional groupings (toss pairs) with syntactical dependencies cannot be considered as freely or randomly selectable, but are subject to determinate rules of syntactic possibility or impossibility. If, on the basis of the existing configuration of a DNA molecule, certain possibilities of change are excluded (i.e., not excluded per se, but only by virtue of the fact that their new appearance would result in some form of syntactic conflict with the existing arrangement) then resulting changes will be to a large extent those occurring due to a system of structural selection based upon their appropriateness to the current configuration; which implies that it is quite misleading to conceive of those changes as occurring randomly and indeterminately.

Survival of the Possible

The point has been made above that the assumption of randomness in genetic mutation relies upon the presumption of rational equivalence between DNA elements; i.e., that there is nothing except chance (and the inherited results of prior chance) that determines the selection and arrangement of DNA coded elements. DNA does not, according to this model, have any capacity for internal selection. To extend the analogy with verbal language, the suggestion is that the system is something like picking individual letters of the alphabet out of a hat, where there is no greater chance for any particular letter to follow any other. But in a symbolic system where the elements are codified syntactically (and in DNA there is not only a linear syntax, but also a three-dimensional syntax), they lose that rational equivalence – they start to develop special affinities for one other, in a sense they become ‘conventional’, and also to an extent ‘irrational’. Think of the frequent pairings and associations that develop between words and letters in a language, for no clear logical or semantic purpose. One would be hard-pushed to find a logical or a semantic explanation for why i must come before e, except after c; or why double consonants are sometimes necessary, where in other cases a single might suffice; or why, for instance, I voice my opinion, but must rather speak my mind.

Lacan’s experiment reproduced above suggests that in so far as a symbolic system entails functional (‘semantic’) groupings of two or more elements in a coded matrix, that there arises a tendency towards affinity between code elements, independently of the semantic purpose for which the code is employed. Language selects – to an extent the choice of words is made for us – according to syntactic determinants internal to language. There are factors in the deep structure of the code that determine my use and selection of code elements which are not apparent to me, and are not affected by semantic concerns, or the meaning that I am trying to construct. For all practical purposes – the ‘intentional’ applications of the code – the determinants of these affinities remain unconscious, and for this reason they are resistant to routine empirical observation and rational causal interpretation. My argument is that something of this kind also operates within DNA, in the syntactic dependencies between AGCT groups in DNA molecules.

It is a characteristic of rationality to think in terms of diametrical oppositions, and the opposition of randomness/non-randomness (in other words chaos/order) is typical of this tendency. To move from randomness to non-randomness, one has to leap across the rational divide, and from a rational perspective these positions are mutually exclusive – the opposing position always appears untenable. The distinction between randomness and non-randomness is not relevant or helpful to an understanding of what happens in the process of genetic change. For evolutionary biology, the assertion of randomness operates as an occlusion of thought, as a kind of ‘event horizon’ of the understanding. There are ways in which genetic changes are determined from within DNA that we don’t fully understand, and which are not reducible to explanation in purely functional terms; however the reliance upon entrenched orthodoxies formulated on the basis of 150-year-old scientific prejudice does nothing to advance that understanding. A further problem with this received dichotomy is that it reinforces the linear-sequential conception of DNA structure. To avoid the rational dichotomy, and also to acknowledge in principle the three-dimensional characteristics of DNA ordering, it may be helpful to rethink the distinction between randomness/non-randomness instead in terms of pre-structure and structure, as these categories are no longer diametrical opposites.

If DNA is a symbolically encoded system, exhibiting functional elements that are internally recognisable, then there is a degree of mathematical inevitability that the code itself will generate its own patterns. This is in the nature of language, whether natural (spoken) languages, or artificial (coded) ones. This is not to suggest that there is any form of conscious ‘intelligent design’, either within or outside of DNA, in the way that it tends to be caricatured by the opponents of religion. The code itself is tendentious; that is to say, the ‘dice’ are already loaded, and that is all that is required to undermine the insistence on the perceived randomness of genetic mutation, and therefore of the primacy of Darwinian natural selection – that is, of the ‘survival of the fittest’ – as the sole arbiter of evolutionary change.

February 2015
(revised 17 February 2023)

back to top ^

Footnotes:

1. James, W., Great Men and their Environment – a lecture before the Harvard Natural History Society; published in The Atlantic Monthly, vol. 46, no. 276, October 1880, pp. 441-459. [back]
2. Gould, S., The Structure of Evolutionary Theory, Harvard, 2002. [back]
3. Gould, S., Betting On Chance – and No Fair Peeking, in his The Richness of Life, McGarr, P. & Rose, S. (eds.), Vintage, 2007, p.167. [back]
4. It is difficult to dismiss here the factor of a certain emotive response to the observation of mutation and deformity, particularly for those occurring within the human population – that is, in the context of a 19th Century moral climate, as exemplified in its attitude towards ‘freaks’ – so that the theory of natural selection emerges imbued with an implicit (moral) tendency toward the selection of ‘good forms’, and the de-selection of the implicitly ‘evil forms’ of deformity. [back]
5. Stott, R., Darwin and the Barnacle, Faber & Faber, 2003. [back]
6. Ibid., p.150. For further discussion of analogies between the habits of financial and theoretical speculation, and on the role of excitement, in the shaping of Darwin’s hypotheses, see ch.7: On Speculating, ibid., pp.135-153. [back]
7. Lewontin, R.C., The Doctrine of DNA: Biology as Ideology, Penguin, 1993, pp.9-10. [back]
8. See: Gould’s Challenges to Neo-Darwininism and Their Meaning for a Revised View of Human Consciousness, in his The Richness of Life, (op cit., pp.222-237). See also: Schweber, S., The Origin of the Origin Revisited, in Journal of the History of Biology, 10 (1977), pp.229-316. [back]
9. Darwin, C., The Expression of the Emotions in Man and Animals (1872), in Darwin: The Indelible Stamp, Watson, J. (ed.), Running Press, 2005, pp.1061-1257. [back]
10. See: Chapter 2 (pp.14-22) and Appendices 1 & 2 of Fink’s: The Lacanian Subject: Between Language and Jouissance, Princeton, 1995 [Google Books preview], for an accessible representation of some of the findings of Lacan’s original experiment, although the full extent of that experiment is considerably more detailed and complex than I can possibly do justice to here. The original references from Lacan are: Seminar II: The Ego in Freud’s Theory and in the Technique of Psychoanalysis (1954-55), Tomaselli, S. (trans.), Miller, J. A. (ed.), Norton & Co., New York, 1991, chs. 15 & 16, pp.175-205; and Seminar on “The Purloined Letter”, in Écrits, Fink, B. (trans.), Norton & Co., New York, 2006, pp.11-48. [back]
11. Fink, op cit., p.19 [back]
12. Ibid. [back]

• BRIEF

  • In Brief..
  • Contact Us
  • A Sitemap

• REPORT

  • SOMR – MRI Evidence
  • 2nd MRI Head Scan
  • C-Spine MRI Scan (July 2020)
  • Concealed Devices
  • Further Evidence
  • Full MRI Scan Downloads
  • Technological Imperatives
  • Complaint to the GMC
  • Complaint to GSTT NHS
  • Attempts on My Life
  • Complaint to Metpolice & IPCC
  • Political Asylum Applications
  • A Miscarriage of Civil Justice
  • Applications to ECtHR
  • Swedish Asylum Applications

• RFR

  • RFR: Research Papers
  • RFR: Effects on Wildlife

• XCETERA

  • The Limits of Rationality
  • Radical Affinity & Variant Proportion in Natural Numbers
  • Is Artificial Intelligence a Fallacy?
  • Mind: Before & Beyond Computation
  • Fifty Shades of Digital
  • Integers & Proportion
  • Intuitive Periodicity in Numerical & Temporal Sequence
  • Quantum Elevations [pdf]
  • Somatic Inscription (growing up with numbers)
  • Dawkins' Memetics – A Biological Assault on the Cultural
  • Randomness, Non-Randomness, & Structural Selectivity